Современная математическая физика:
струны и гравитация, суперсимметрия, интегрируемость
| Руководители темы: |
Исаев А.П.
Сорин А.С.
Кривонос С.О. |
|
| Научный руководитель темы: |
Филиппов А.Т. |
Участвующие страны и международные организации:
Австралия, Австрия, Армения, Болгария, Бразилия, Великобритания, Венгрия, Германия, Греция, Индия, Испания, Италия, Канада, Люксембург, Норвегия, Польша, Россия, Румыния, Сербия, США, Турция, Украина, Франция, ЦЕРН, Чехия, Япония, ICTP.
Изучаемая проблема и основная цель исследований:
Целью исследований в области математической физики является разработка математических методов решения важнейших проблем современной теоретической физики, а именно - прояснение природы фундаментальных взаимодействий и их симметрий, построение и изучение эффективных полевых моделей, возникающих в теории струн и других протяженных объектов, решение проблем геометрического описания квантовых симметрий и их спонтанного нарушения, а также построение единой теории всех фундаментальных взаимодействий, включая квантовую теорию гравитации. Математическая физика в последние годы характеризовалась возрастающим интересом к выявлению и эффективному использованию свойств интегрируемости в различных ее областях, применению мощных математических методов квантовых групп, суперсимметрии и некоммутативной геометрии как в квантовых теориях фундаментальных взаимодействий, так и в классических моделях. При решении задач темы решающим фактором будет использование этих методов.
Ожидаемые результаты по завершении этапов темы:
- Развитие новых математических методов для описания разнообразных интегрируемых моделей и их точных классических и квантовых решений.
- Анализ широкого круга задач теории суперструн и супербран, включая исследование непертурбативных режимов суперсимметричных калибровочных теорий.
- Построение микроскопического описания черных дыр и развитие космологических моделей ранней Вселенной.
Ожидаемые результаты по этапам темы в текущем году:
- Исследование топологии и геометрии многообразий модулей специальных бор — зоммерфельдовых лагранжевых циклов в алгебраических многообразиях.
Построение канонических расслоений Берри на многообразиях модулей специальных бор — зоммерфельдовых лагранжевых циклов в алгебраических многообразиях.
Построение голографических ренормгрупповых потоков связанных с SL(2,C) цепочкой Тоды. Анализ построенных РГ потоков в контексте дуальности калибровочная теория/гравитация.
Поиск решений без горизонта (бозонные звезды) с асимптотикой в виде пространства анти де-Ситтера и анизотропных пространств. Анализ найденных решений в рамках голографического подхода.
Построение решений Керра-Вадьи и Керра-Ньюмена-Вадьи с асимптотикой в виде пространства AdS для D=5 голографической модели. Изучение локальных операторов (двухточечных корреляторов) для найденных метрик в голографическом подходе.
Применение обобщенной формулы Решетихина для скалярных произведений векторов Бете в задачах вычисления форм-фактров локальных операторов в квантовых интегрируемых моделях с симметриями высокого ранга. Получение детерминантных формул для таких средних и их применение в вычислениях корреляционных функций локальных операторов в термодинамических пределах.
Построение классических интегрируемых систем на многообразиях модулей пре-проективных алгебр и их приложение к обобщённым иерархиям КП. Построение квантовых интегрируемых деформированных эллиптических систем Калоджеро–Мозера с помощью эллиптических операторов Данкла. Построение собственных функций деформированных систем Макдональда–Руджинарса с помощью теории представлений алгебры Динга–Иохары.
Исследование систем осцилляторов, инвариантных относительно деформаций алгебры Галилея (включающих большинство некомпактных простых алгебр Ли). Показать, что для любых алгебр есть возможность построить системы со стандартными линейными уравнениями гармонического осциллятора и осциллятора Пайса-Уленбека. Применить полученные результаты к некоторым частным случаям, в т.ч. G2.
Исследовать N=4 суперсимметричные механики многих частиц на искривленных пространствах: найти обобщения условий, которые определяют существование суперзарядов, в т.ч. уравнения WDVV для искривленных пространств, условия на допустимые потенциалы, найти их частные решения.
Построение точного решения квантовой задачи гармонического осциллятора на двухполостном гиперболоиде SO(3,1)/SO(3) в четырех системах координат: сферической, полярно-цилиндрической, эквидистантно цилиндрической и эквидистантой. Нахождение коэффициентов межбазисных разложений между данными системами координат. Также планируется полное решение классических задач Кеплера- Кулона и гармонического осциллятора на однополостном гиперболоиде SO(3,1)/SO(2,1) методом решения уравнений Гамильтона-Якоби, и построение траекторий движения.
Изучение компактных объектов в модифицированных теориях гравитации и определение из наблюдательных и экспериментальных данных массы дополнительного скалярного поля.
Развитие новых методов обработки и анализа наблюдательных данных, получаемых детекторами гравитационных волн.
Развитие теории и приложений функций Гойна в проблемах математической физики и теории гравитации.
- Будут произведены 2-х петлевые расчёты в N=(1,1) 6D суперсиммеричной теории Янга-Миллса в подходе гармонического суперпространства: выяснен вопрос с ультрафиолетовыми расходимостями и конечными вкладами в суперполевое эффективное действие. Будут построены все независимые инварианты канонической размерности d=12 и рассмотрены возможные применения этих инвариантов (и инвариантов более высокой размерности) для построения 6D теории Борна-Инфельда с явной N=(0,1) и скрытой N=(1,1) 6D суперсимметриями.
Будут построены и исследованы новые SU(2|2) и SU(4|2) суперсимметричные расширения моделей Калоджеро-Мозера как деформации N=4 и N=8 суперсимметричных расширений, исследован вопрос их интегрируемости и связи с матричными моделями теории струн.
Изучение моделей 6D супергравитации в N=(1,0) и N=(1,1) 6D гармонических суперпространствах, соответственно, на массовой поверхности и вне её. Связи N=(1,1) 6D супергравитации будут решены в терминах N=(1,0) суперполей.
Построение суперполевых действий для многочастичных систем с N=4 и N=8 деформированными суперсимметриями. Суперполевая формулировка сигма-модели с членом Весса-Зумино, обладающей N=4 и N=8 деформированными суперсимметриями и описывающей взаимодействие спиновой частицы с внешним калибровочным фоном.
Построение моделей спиновых частиц и суперчастиц с использованием импульсных твисторов. Получение амплитуд перехода методом BFV–BRST функционального интеграла.
Определение геометрий, описываемых N=4 суперсимметричными квантово-механическими сигма-моделями с разнообразными динамическими, полудинамическими и калибровочными супермультиплетами. Определение вида суперзарядов для различных геометрий.
Построение новых решений типа "волосатых" черных дыр, связанных с заряженным скалярным конденсатом в пространстве Керра-Ньюмена. Исследование гравитирующих Скирмионов в пределе Богомольного. Построение вращающихся "лохматых" черных дыр в модели Скирма в пределе Богомольного.
- Изучение различного вида граничных эффектов в конформных теориях, таких, например, как силы Казимира, и их возможного голографического представления в дуальных теориях гравитации с целью понять особенности данных эффектов в режиме сильной связи. Будет выполнен расчет энергии Казимира в свободных конформных теориях в пространствах с размерностью D=3,4,6. для различных конфигураций границ с граничными условиями, не нарушающими конформную инвариантность. В 4-мерном случае соответствующей теорией является суперсимметричная теория Янга-Миллса. Результаты будут использованы для определения того, какие из вариантов голографического описания конформных теорий с границами способны воспроизвести энергию Казимира.
Будут исследованы вакуумные флуктуации квантовых полей (спинорного и векторного) в присутствии решеток многомерных дельта-функций. Подобные двумерные периодические системы последнее время привлекают внимание в связи с описанием дисперсионных сил между поляризуемыми листами, например между листами графена. Эта деятельность связана с развитием теории само-сопряженных расширений операторов, а также со спектральной геометрией, а именно, с построением спектральных дзета-функций и асимптотического разложения теплового ядра дифференциальных операторов на сингулярном фоне или с сингулярным потенциалом.
Методом двухвременных температурных функций Грина будет рассчитана сила вакуумного трения между макроскопическими телами с учетом всех порядков по относительной скорости тел.
Будет продолжено изучение фазовой структуры в некоторых реалистичных моделях f(R)-гравитации. Будет вычислен спектр космологических возмущений в этих теориях.
Будут исследованы модели скалярно-тензорной телепараллельной гравитации и вычислены спектры космологических возмущений в рамках этих теории.
Изучение модели гравитации, основанной на нелинейной реализации совместной аффинной и конформной симметрии, изучение квантовых свойств теории, свойств перенормируемости в первом и втором порядке теории возмущений.
Изучение свойств теорий гравитации класса Horndeski.
Изучение масс-инфляции на горизонтах Коши черных дыр в зависимости от наличия электрического и магнитного зарядов, углового момента и скалярных волос, как в теории гравитации Эйнштейна, так и в случае неминимальной связи между материей и гравитацией. Изучение масс-инфляции необходимо для прояснения фундаментальных вопросов, связанных с наличием сингулярностей в решениях теорий гравитации.
Исследование неминимального взаимодействия типа Хорндески для полей Максвелла и Янга Миллса применительно как к черным дырам, так и к космологии, где оно особенно привлекательно благодаря свойству лагранжиана вырождаться на фоне метрики Де Ситтера определенного радиуса кривизны. Недавно нами показано, что присутствие такого квазиаттрактора приводит к естественному возникновению инфляционного режима конечной протяженности во времени в модели Фридмана с полем SU(2). Будут продолжены эти исследования, в том числе в формализме первого рода (т.н. формализм Эйнштейна-Палатини), при котором связность трактуется как независимая переменная при варьировании действия. Для теорий с неминимальной связью между материей и гравитацией нет оснований априори считать связность согласованной с метрикой, что приводит к отличающимся динамическим моделям с другими пространствами решений.
Будут изучены точные решения Стефани с переменной пространственной кривизной, их возможное влияние на инфляционную космологию и общие топологические свойства. Будет изучен вопрос о космологическом горизонте в модели вакуоли Эйнштейна-Страуса и модели Леметра-Толмана-Бонди.
Будут рассмотрены перспективы формирования структур в неоднородных моделях, оценены наблюдаемые космологические параметры и обработаны экспериментальные данные. Космологические модели Стефани и 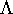 CDM будут сравниваться с феноменологической точки зрения.
CDM будут сравниваться с феноменологической точки зрения.
Будет проанализирована конформная гравитация Маннгейма, будут получены кривые галактического вращения без присутствия темной материи в свете современных космологических измерений. Будет изучена внутренняя структура теории Мангейма, проблемы с унитарностью и ее критическая оценка как возможного кандидата квантовой гравитации.
| Основные этапы темы: |
| |
Этап темы |
Руководители |
|
| |
Лаборатория или другие
подразделения ОИЯИ |
Основные исполнители |
1. Квантовые группы и
интегрируемые системы |
Исаев А.П. |
|
| |
ЛТФ
|
Голубцова А.А., Кривонос С.О., Козырев Н.Ю., Митрюшкин В.К., Петросян Д.Р., Погосян Г.С., Силантьев А.В., Тюрин Н.А., Физиев П., Фукса Я. + 1 студент |
| 2. Суперсимметрия |
Иванов Е.А. |
|
| |
ЛТФ
|
Пентек М.Р., Петрыковски А, Самсонов И.Б., Сидоров С.С., Сутулин А.О., Федорук С.А., Шнир Я.М. |
3. Квантовая гравитация,
космология и струны |
Филиппов А.Т.
Нестеренко В.В.
Сорин А.С. |
|
| |
ЛТФ
|
Барбашов Б.М., ормотова И., Давыдов Е.А., Латош Б.Н., Пестов А.Б., Пироженко И.Г., Тагиров Э.А., Третьяков П.В., лувкова П. + 3 студента |
| |
ЛИТ
|
Боголюбский И.Л., Червяков А.М. |
| Сотрудничество по теме: |
|
Страна или
международная
организация |
Город |
Институт или
лаборатория |
Участники |
Статус |
| Армения |
Ереван |
ЕГУ |
Нерсесян А.П. |
Совместные работы |
| |
|
|
Гурзадян В. |
Совместные работы |
| |
|
|
|
Совместные работы |
| Болгария |
София |
INRNE BAS |
Тодоров И.Т. + 2 чел.
Илиев Б.
Молотков В.
Добрев В. |
Обмен визитами |
| |
|
SU |
Чижов М.В.
Бояджиев Т. |
Обмен визитами |
| Польша |
Варшава |
NCAC PAS |
Манкиевич Л. + 1 чел. |
Обмен визитами |
| |
|
UW |
Воронович С.
Бодзента-Скибинска А. |
Обмен визитами |
| |
Вроцлав |
UW |
Лукерски И. + 3 чел.
Попович З.
Фридришак А.
Боровец А. |
Совместные работы |
| |
Краков |
JU |
Ародзь Г. + 2 чел. |
Обмен визитами |
| |
|
NINP PAS |
Хожеля А. + 1 чел. |
Обмен визитами |
| |
Лодзь |
UL |
Тыбор В. |
Обмен визитами |
| Россия |
Москва |
ВНИИМС |
Иващук В.
Мельников В. |
Обмен визитами |
| |
|
ГАИШ МГУ |
Топоренский А.В.
Алексеев С.О. |
Обмен визитами |
| |
|
ИТЭФ |
Морозов А.Ю. + 4 чел.
Ольшанецкий М.А.
Черняков Ю.Б.
Рослый А. |
Обмен визитами |
| |
|
МГУ |
Гальцов Д. + 2 чел.
Шафаревич А.
Жеглов А.
Свешников К.А. + 2 чел.
Панов Т.
Талалаев Д.В. |
Обмен визитами |
| |
|
|
|
Совместные работы |
| |
|
МИАН |
Славнов А.А. + 3 чел.
Орлов Д.
Арефьева И.Я. + 2 чел.
Волович И.В.
Катанаев М.
Кузнецов А.Г.
Славнов Н.А. |
Обмен визитами |
| |
|
|
|
Совместные работы |
| |
|
НИУ ВШЭ |
Пушкарь П.Е. |
Обмен визитами |
| |
|
РУДН |
Скугорева М.А. |
Обмен визитами |
| |
|
ФИАН |
Барвинский А. + 1 чел.
Васильев М.А. + 2 чел.
Манько В.И. + 1 чел. |
Обмен визитами |
| |
Москва, Троицк |
ИЯИ РАН |
Березин В.
Рубаков В.А. + 2 чел.
Горбунов Д.С. |
Обмен визитами |
| |
Долгопрудный |
МФТИ |
Ждановский И. |
Обмен визитами |
| |
Казань |
КФУ |
Сушков С.В. |
Обмен визитами |
| |
Новосибирск |
НГУ |
Миронов А. |
Обмен визитами |
| |
Протвино |
ИФВЭ |
Пронько Г.П.
Разумов А. |
Обмен визитами |
| |
С.-Петербург |
ПОМИ РАН |
Деркачев С.Э. + 2 чел. |
Обмен визитами |
| |
|
СПбГУ |
Прохоров Л.В. + 1 чел. |
Обмен визитами |
| |
Томск |
ТПУ |
Галажинский А.В.
+ 3 чел. |
Совместные работы |
| |
|
ТГПУ |
Бухбиндер И.Л. + 4 чел.
Ойконому В.К. |
Совместные работы |
| |
Черноголовка |
ИТФ РАН |
Белавин А.
Соколов В.В.
Шабат А.Б.
Старобинский А.А. |
Обмен визитами |
| Румыния |
Бухарест |
IFIN-HH |
Вишинеску М. + 2 чел. |
Совместные работы |
| Украина |
Киев |
ИТФ НАНУ |
Шадура В.Н.
Йоргов Н.З.
Ляшик А.В. |
Обмен визитами |
| |
|
|
|
Совместные работы |
| |
Харьков |
ННЦ ХФТИ |
Желтухин А.А.
Гершун В.
Нурмагомбетов А.
+ 2 чел. |
Совместные работы |
| Чехия |
Прага |
CTU |
Главаты Л.
Бурдик Ч. + 3 чел. |
Обмен визитами |
| |
|
CU |
Горжейши И. + 1 чел. |
Обмен визитами |
| |
Опава |
SlU |
Стухлик З. |
Совместные работы |
| |
Ржеж |
NPI ASCR |
Труглик Э. + 2 чел.
Диттрих Я. |
Обмен визитами |
| Венгрия |
Будапешт |
Wigner RCP |
Нири Ю.
Френкель А.
Гогохия В.Ш. + 1 чел. |
Обмен визитами |
| Германия |
Берлин |
FU Berlin |
Кляйнерт Х. + 2 чел. |
Соглашение |
| |
|
MBI |
Интравайа Ф. |
Совместные работы |
| |
Билефельд |
Ун-т |
Лаерман Е. + 1 чел. |
Соглашение |
| |
Бонн |
UniBonn |
Гелен Г.
Риттенберг В.
Манин Ю.И. + 1 чел. |
Соглашение |
| |
Ганновер |
LUH |
Лехтенфельд О. + 2 чел.
Драгон Н. + 2 чел. |
Соглашение |
| |
Дортмунд |
TU Dortmund |
Глюк М. + 2 чел. |
Соглашение |
| |
Йена |
Ун-т |
Баслер М. + 1 чел.
Штробль Т.
Мохаупт Т. |
Соглашение |
| |
Лейпциг |
UoC |
Бордаг М. |
Совместные работы |
| |
Мюнхен |
MPI-P |
Люст Д. + 4 чел.
Лопес-Кардозо Г.
Аскьери П. |
Соглашение |
| |
Ольденбург |
IPO |
Грунау С. |
Совместные работы |
| |
Потсдам |
AEI |
Тейзен С.
Николаи Х.
Резолла Л. |
Соглашение |
| Италия |
Бари |
INFN |
Нардулли Г. + 1 чел. |
Соглашение |
| |
Неаполь |
INFN |
Бучело Ф.
Миеле Дж. |
Совместные работы |
| |
Павия |
INFN |
Швацер П. |
Совместные работы |
| |
Падуя |
UniPd |
Бассетто А.
Пасти П.
Сорокин Д. |
Соглашение |
| |
Пиза |
INFN |
Ди Джакомо А. + 2 чел.
Менотти П.
Минчев М. |
Соглашение |
| |
Салерно |
UNISA |
Скарпетта Г. |
Соглашение |
| |
Триест |
SISSA/ISAS |
Бонора Л. + 1 чел.
Дубровин Б.А. + 1 чел. |
Обмен визитами |
| |
Турин |
UniTo |
Фре П. + 2 чел.
Кастеллани Л.
Д'Адда + 1 чел. |
Совместные работы |
| |
Фраскати |
INFN LNF |
Беллуччи С. + 2 чел. |
Соглашение |
| Сербия |
Белград |
IPB |
Драгович Б. + 1 чел. |
Совместные работы |
| |
|
Ун-т |
Благоевич М.
Саздович Б.
Шлячки Д. |
Обмен визитами |
| Австралия |
Перт |
UWA |
Кузенко С. + 2 чел. |
Совместные работы |
| |
Сидней |
Ун-т |
Молев А. + 1 чел. |
Соглашение |
| Австрия |
Вена |
TU Wien |
Гроссе Х. |
Обмен визитами |
| Бразилия |
Жуис-ди-Фора |
UFJF |
Шапиро И.Л. |
Совместные работы |
| |
Сан-Паулу |
USP |
Ривеллес В.
Томио Л. |
Совместные работы |
| Великобритания |
Лондон |
Imperial College |
Стелл К. + 2 чел. |
Обмен визитами |
| |
Брайтон |
US |
Калмет Х. |
Обмен визитами |
| |
Глазго |
U of G |
Фейгин М.В.
Бахамонде С. |
Совместные работы |
| |
|
|
|
Обмен визитами |
| |
Дарем |
Ун-т |
Закревски В. + 2 чел. |
Обмен визитами |
| |
Йорк |
Ун-т |
Корриган Э. + 1 чел. |
Обмен визитами |
| |
Кембридж |
Ун-т |
Гиббонс Г. + 1 чел.
Вильямс Р. |
Обмен визитами |
| |
Ливерпуль |
Ун-т |
Джонс Т.
Джак И. |
Обмен визитами |
| |
Лидс |
UL |
Чалых О.А. |
Обмен визитами |
| |
|
|
|
Совместные работы |
| |
Саутгемптон |
Ун-т |
Росс Д.
Стивен Н.Г. |
Обмен визитами |
| Греция |
Афины |
UoA |
Зупанос Дж. + 1 чел. |
Совместные работы |
| Индия |
Калькутта |
BNC |
Гангопадхья Д. + 2 чел. |
Соглашение |
| |
|
IACS |
Коушик Р. |
Соглашение |
| |
Ченнай |
IMSc |
Мухопадхья П. |
Соглашение |
| Испания |
Мадрид |
ETSIAE |
Кастаньеда Х.М.М. |
Обмен визитами |
| |
|
|
|
Совместные работы |
| |
Бильбао |
UPV/EHU |
Бандос И. |
Обмен визитами |
| |
|
|
|
Совместные работы |
| |
Барселона |
IEEC-CSIC |
Одинцов С.Д. |
Обмен визитами |
| |
|
|
|
Совместные работы |
| |
Валенсия |
IFIC |
Де Азкаррага Х.А. |
Обмен визитами |
| |
|
|
|
Совместные работы |
| Канада |
Ванкувер |
TRIUMF |
Бэггер Дж. |
Совместные работы |
| |
Монреаль |
McGill |
Контогорис А. + 1 чел. |
Обмен визитами |
| |
|
UdeM |
Винтерниц П. |
Совместные работы |
| |
Эдмонтон |
U of A |
Фролов В.
Пейдж Д. |
Совместные работы |
| Люксембург |
Люксембург |
Ун-т |
Шлихенмайер М. |
Обмен визитами |
| Норвегия |
Тронхейм |
NTNU |
Бревик И. |
Совместные работы |
| США |
Нью-Йорк |
CUNY |
Акулов В.
Корепин В. |
Обмен визитами |
| |
|
RU |
Эванс М. |
Обмен визитами |
| |
|
SUNY |
Ван Ньевенхойзен П. |
Обмен визитами |
| |
Колледж Парк |
UMD |
Гэйтс Дж. |
Обмен визитами |
| |
Корал Габлс |
UM |
Мезинческу Л. + 2 чел. |
Совместные работы |
| |
Миннеаполис |
U of M |
Вайнштейн А. + 2 чел. |
Обмен визитами |
| |
Норман |
OU |
Милтон К. |
Совместные работы |
| |
Пискатавей |
Rutgers |
Замолодчиков А.Б.
+ 1 чел. |
Обмен визитами |
| |
Рочестер |
UR |
Дас А. |
Обмен визитами |
| |
Филадельфия |
Penn |
Сарафян Г. + 1 чел. |
Обмен визитами |
| |
Цинциннати |
UC |
Шураньи П. + 1 чел. |
Совместные работы |
| Турция |
Стамбул |
BU |
Арик М.
Огаз О. |
Совместные работы |
| |
Измир |
IZTECH |
Таноглу Г.
Атылган Ш. |
Совместные работы |
| Франция |
Париж |
ENS |
Казаков В.А.
Поликастро Дж. |
Обмен визитами |
| |
|
|
|
Совместные работы |
| |
|
LPTHE |
Дюбуа-Виолетт М.
Шифф Д. + 2 чел. |
Обмен визитами |
| |
|
LUTH |
Гургуйон Э. |
Совместные работы |
| |
Аннеси-ле-Вье |
LAPP |
Сокачев Э.
Сорба П.
Рагоси Э. |
Обмен визитами |
| |
|
|
|
Совместные работы |
| |
Анжер |
LAREMA UA |
Рубцов В. |
Совместные работы |
| |
Валансьен |
UVHC |
Гуревич Д. |
Совместные работы |
| |
Дижон |
IMB |
Китанин Н.
Козловский К. |
Совместные работы |
| |
|
UB |
Матвеев В. + 1 чел.
Штернхаймер Д. |
Обмен визитами |
| |
Лион |
ENS Lyon |
Дельдук Ф.
Майе Ж.М. |
Совместные работы |
| |
Марсель |
CPT |
Соффер Ж. + 2 чел.
Кокоро Р.
Огиевецкий О.В. |
Совместные работы |
| |
Нант |
SUBATECH |
Смилга А. |
Соглашение |
| |
|
|
|
Обмен визитами |
| |
Палезо |
Polytech |
Пире Б. |
Совместные работы |
| ЦЕРН |
Женева |
ЦЕРН |
Венециано Г.
Альварец-Гоме Л. + 2 чел.
Антониадис И. + 1 чел.
Феррара С. + 2 чел. |
Соглашение |
| Япония |
Токио |
UT |
Сираиси Д. |
Обмен визитами |
| |
Касива |
Kavli IPMU |
Саито К. |
Обмен визитами |
| |
Киото |
KSU |
Согами И. + 1 чел. |
Обмен визитами |
| |
|
RIMS |
Мива Т.
Оджима И. |
Обмен визитами |
| |
|
YITP |
Матсуи Т. + 1 чел.
Увано И. |
Обмен визитами |
| |
Фукуока |
Kyushu Univ. |
Накаяшики А. |
Обмен визитами |
| |
Фукусима |
Fukusima Univ. |
Казухара Б.
Бамба К. |
Обмен визитами |
| |
Цукуба |
KEK |
Кобаяши М. |
Обмен визитами |
| ICTP |
Триест |
ICTP |
Ранджбар-Даэми С. |
Соглашение |
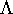 CDM будут сравниваться с феноменологической точки зрения.
CDM будут сравниваться с феноменологической точки зрения. 